おとなも学ぶ、数学の時間。
数年ぶりに、第3回目の「おとなの かずの不思議」を9月29日に開催しました。その趣旨は、数理的な現象の不思議さと美しさを学園の子どもだけでなくおとなも楽しもうということです。
1.パスカルの三角形 2.三角数と四角数 3.フィボナッチ数 の3つの内容に8名の方々が参加されました。
はじめに 全員がお互いの自己紹介をしました。殆どの方が算数や数学への苦手意識や、しばらく数の世界から遠ざかっていたが、数の世界に関心があって参加したとのことでした。

私はそれに対して、日本の算数・数学教育は和算の影響で、問題の提示 →その解法 → 解法の習熟 がメインの流れになってきたので、わが国では年齢とともに数への関心が薄れ、数の世界から遠ざかる傾向がある。しかし、本来子どもがもつ数に対する好奇心や不思議の種を基に遊びの感覚で接していけば、数に親しみつつ数の世界に自然に入っていけるのではないか、私はこれまでずっとその信念で算数・数学教育に携わってきたことをお話ししました。そのついでに「今ネットで話題の“おみやげざん”のことをご存じですか?」と尋ねたところ、全員が「知らない」とのことでしたので、急遽予定を変更しておみやげざんの話題から入りました。
簡単に暗算できてしまう、おみやげざん
おみやげざん これは 17×18, 21×26, 86×87 のような10の位が同じ2桁の数の掛算を簡単なメモか暗算で済ます方法です。例えば、17×18 は、17の7をおみやげとして、後ろの18に渡すと、計算式は10×25に変わり、これから直ぐ250、次いで1の位の7と8を掛けると56、これらから 250+56=306(←17×18の答え)。全員に電卓を配布して確認してもらいました。
学園では 15×15, 25×25, 85×85 のような10の位が同じで1桁目が5の2桁の数の掛算と、
17×13, 24×26,82×88 のような10の位が同じで1桁目の数の和が10になる2桁の数の掛算を暗算でやる方法を紹介し、その仕組みを伝えたことがあります。いずれも中学で学ぶ公式
(x+a)(x+b)の活用です。なお、当時はおみやげざんに私は気付いていませんでした。

不思議な秘密が隠れている、パスカルの三角形
(1)パスカルの三角形
先ず次頁の空欄を埋める作業を進めてもらいました。上から2段目の左右の1を足してできる2を3段目の空欄に書き込み、4段目の左右の空欄には、両端の1といま書き込んだ2を足してできる3, 3と記入します。同様にして4段目の空欄には4,6,4と記入します。全員の方が10段目近くまで黙々と作業を進められました。

このようにして生まれる数の三角形を「パスカルの三角形」いいますが、「この表には数の秘密が隠れています」と伝えたところ、しばらく観察してから数名の手が上がりました。
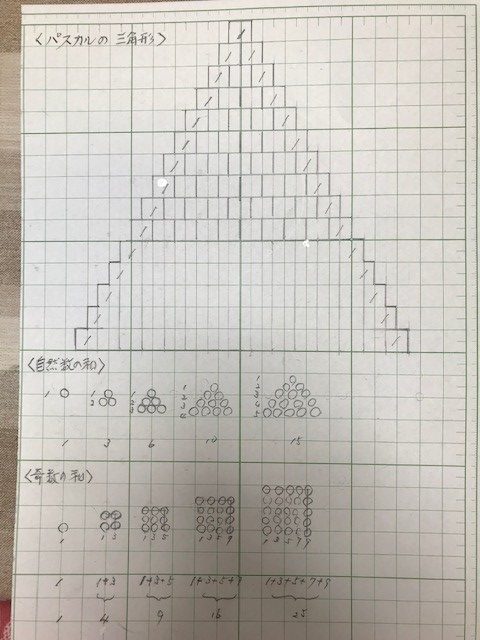
いまこのブログをお読みの方は、10段目近くまで数を埋める作業をやって、自分で「表の秘密」の発見を試みられることをお勧めします。
当日みなさんが最初に気付かれたのは「自然数の列の出現」でした。(次頁の ①) それはなぜか? 2つの数の和を、その直ぐ下の空欄に書き込んでいったからです。(ピンときましたか?)
ここからさらに秘密の考察を進める準備として、新しい話題に移りました。
図形と数の不思議な関係。
(2)三角数と四角数
上表の下半分には、すでに <自然数の和> 、<奇数の和> の見出しに続いて ○が連続して並んでいます。当日は空欄のまま配布して各人が○を描き、その全体の形状から、それぞれ「三角数」、「四角数」と命名されていることをお伝えしました。
(参加されていたみなさんに、最初<奇数の和の個所>を、私の勘違いで誤記していたことをお詫びします)
さらに、パスカルの三角形を下図のように、斜め①の列と 斜め②の列を意識し、さらに各段の数の和を右に書き出してみると、 ①は自然数の列、②は自然数の和の列=三角数の列、また各段の数の和は、1+1=2, 1+2+1=4, 1+3+3+1=8, 1+4+6+4+1=16, 1+5+10+10+5+1=32 … となり、何と2の自然数乗(2¹, 2², 2³, 2⁴, 2⁵ …)が整然と並んでいます!
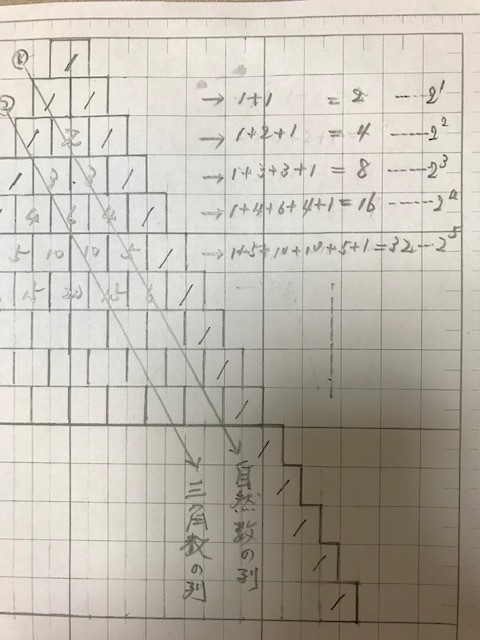
ここまでの展開で、すでに1時間50分を費やしましたが、前もって参加者から強い要望があったフィボナッチ数と黄金分割比の関連を、短時間ながら紹介することにしました。
自然界に存在する数列。
(3)フィボナッチ数列
フィボナッチ数列を作り出すことから始めました。1,1からはじまる連続する2数の和を続けて並べると、数の列は 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 … となりますが、これがフィボナッチ数列です。次に連続2項を前の数で後ろの数を割った結果を次々と電卓で計算してもらうと、
1/1=1,2/1=2, 3/2=1.5,5/3=1.667, 8/5=1.6, 13/8=1.625, 21/13=1.615, 34/21=1.619, …
これらの値は増加と減少を繰り返しながら結局、黄金分割比(1+√5)/2=1.6180339…に接近していくとお伝えしました。 「なぜ、√5がでてくるのか?」と質問がありましたが、残念ながら時間がないためその説明はできずに、今回の数の不思議は終わりました。
もっと知りたい方へ。
(1)(2)(3)のことをもっと知りたい方は、
「数の悪魔」(エンツェンスベルガ-著 丘沢静也 訳 晶文社)をご覧ください。
本書は、日本で50万部も売れた数学児童文学書として珍しいベストセラーだそうです。「数の不思議な現象」の話が、豊富なカラーのイラストを添えて展開されています。こども対象の本として書かれたためか、基本的に証明はなく、不思議な現象の理由は自分で考えるしかありません。
本に記されてはいないですが、実は上記の斜めに並ぶ数の列を、①,②の後に③,④…と続けると、それらすべてに面白い秘密が隠れています!
私はこの夏、パスカルの三角形を中心に数々の不思議の証明を愉しみました。他の項目もそれぞれに興味深い内容でした。機会があればいつかご一緒に楽しみましょう。
以上、アミこと 松崎雅夫 (2024.10.2)

(参加者8名の感想…すべて原文のまま)
1.はじめて知ることばかりで勉強になった。不思議なことを理論立てて説明しくれて助かった。
2.数の不思議から「美しさ」を感じました。好奇心を満たすために学ぶ、その言葉が印象的でした。叉、知らないことだらけで、もっと早く知りたかったです。実生活やくらし、身近なものと結び付けて色々発見していきたいです! 面白かったです。ありがとうございました。
3.数十年ぶりに数学にふれて新鮮でした。フィボナッチは初めて聞きましたが、面白かったです。フィボナッチの話、もっといろいろ聞きたかったです。
4.パスカルの三角形には、いろいろな数列が含まれているので面白いと思った。
パスカルは何故こんなことを考えたのだろうか? 自然界にはフィボナッチになっているものが多いと聞くが代表的なものがあるのか?
5.おみやげ算 知りませんでした。数字と図形の関係が面白いと感じました。フィボナッチ数列は宇宙の摂理なのではと… プラネタリウム番組「MUSCA(ムジカ)」で紹介されていました。
6.面白かったことは、数字の羅列が奇麗な図形をしていたことです。(図を添えて)まるでピラミッドを横から見たり縦から見たりしているようでした。
7.興味深く話をきかせてもらえて楽しい時間でした.数学は積み重ねの学問なので、どこかでつまづくと数学嫌いになってしまい、数学から遠ざかっていました。こうして不思議の世界をのぞきみできて、数学の勉強の意欲がわきました。ありがとうございます。
8.今日初めて参加させて頂き、とても楽しかったです。自然界も数列の法則にのっとったものであると知り、数学の奥深さ、ロマンを感じ、素敵な時間でした。ありがとうございました。
もりラボ企画とは…
「学びは子どものものだけじゃない。おとなも学ぼう。民主的に生きよう。対話を通じて学びを深めよう」
という、おとなの森のコンセプトを、NPO法人コクレオの森の会員のみなさんが主体的に企画し、仲間を集め、実施するイベントです。